GPS 的输出数据如何转化为无人机控制需要的状态信息

下图是国内某知名无人机企业的2014 年笔试的截图，显示了导航过程中的数据转换的实用性。

在之前的文章中，我介绍了无人机系统自动导航过程中涉及的几个重要坐标系，本文则会跟大家分析在实际的无人机系统中，GPS 的输出数据如何转化为无人机控制需要的状态信息。
　　

GPS输出数据详解

实际的 GPS 系统会以一定格式输出很多数据，如时间，精度因子，卫星编号，信噪比等等，但对于无人机控制而言，最为重要，也是最常使用的还是「经度(Longitude)，纬度(Latitude)以及高度(height)」三组数据。
　　

直接通过 GPS 获取的飞行器的位置坐标基于 WGS-84(World Geodetic System-1984)坐标系，简称 Geodetic 或 G 坐标系。

为什么需要单独建立一个坐标系呢?这是由于地球表面地势复杂，有山有海，高低不平。需要建立一个简单而精确的近似数学模型，大家决定采用椭球体作为地球的近似。而 G 坐标系就描述了一个椭球体，给出该椭球体的基本参数：长半轴，短半轴，第一偏心率，第二偏心率，扁率，曲率半径(米)：

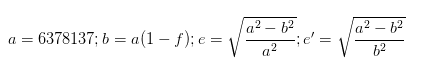
GPS输出的高度不是海拔(Alt)么?这里怎么是 h 高度呢?GPS 硬件直接获取的高度是相对于 G 坐标系中椭球表面的高度。而海拔是相对于公海平面的高度，与地球表面形状和重力分布相关。相对于大地水准面的高度才是海拔，也就是下图中的H参数。

M(大地水准偏差)作为GPS输出高度h和当地海拔之间的偏差，一般在正负100m以内。
　　

从 Geodetic 到 ECEF 坐标系的数据转换
　　

我们通过 G 坐标系下的三个参数：经度，维度，高度，可以获得飞行器在椭球表面的位置坐标。但进行导航计算时，我们需要把数据换算到 NED 坐标系下。要完成从 G 系到 NED 的数据转换还需要一个过渡过程：G 坐标系到 ECEF 坐标系下的数据转换。
　　

其中 N 是我们常说的曲率半径(m)。通过上面的计算公式就可以实现从 G 坐标系到 ECEF 坐标的数据转换。
　　

从ECEF到NED坐标系的数据转换
　　

对于商用无人机，相比于它在椭球中的信息，我们更关心它在平面中的位置向量、速度向量。将 NED 坐标系看做导航中最重要的坐标系并不为过，NED 坐标系也经常被直接称为导航坐标系(Navigation Coordinate)或者地面坐标系(Ground Coordinate)。

首先要获取 NED 坐标系中的参考原点，一般也就是无人机 GPS 星数达到要求后的起始位置。这也是为什么无人机产品要在星数足够之后才能起飞，试想一下如果起始位置没有定准，就算在飞行过程中星数足够，获取的飞行位置信息也够精确，最后也可能造成一键返航位置与起始位置偏差巨大。

下面给出参考原点的坐标信息以及从 ECEF 到 NED 的转换计算：

从ECEF到NED坐标系的旋转矩阵如下： 

结合上面两部分的计算方法，就成功地实现了 GPS 输出的位置数据到 NED 坐标系下的转换。换句话说，我们获得了进行无人机控制器设计所必须的外环位置状态信息。
　　

但外环信息一共有六个，还有三个速度状态呢?通过 GPS 可以获得 ECEF 坐标系下的速度向量。与 G 系类似，相比于飞行器在 ECEF 这个三维坐标系的速度向量，我们更关心相对于 NED 坐标系的速度向量：